SAT - SN P systems

Description

This example gives a solution to the well-known NP-complete problem of SAT, by means of spiking neural P systems, as presented in [1] and adapted to P-Lingua and MeCoSim in [2]. It would be similar to this:

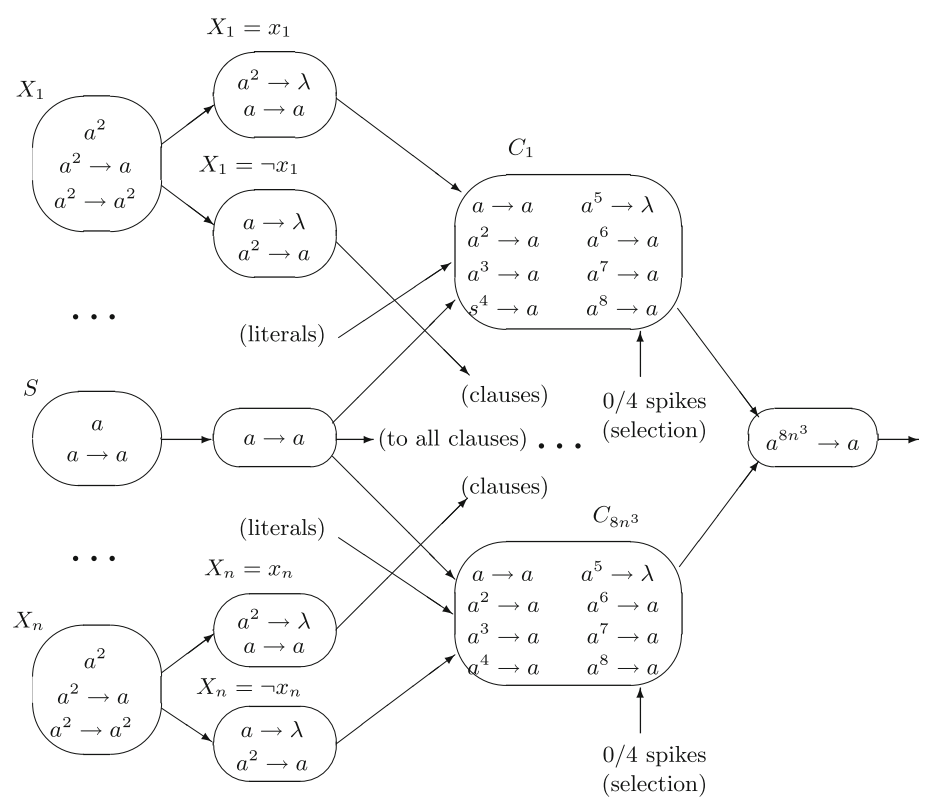
Model

The corresponding P-Lingua file is the following:

@model<spiking_psystems>

def main()
{
        call spiking_init_conf(n,m);
        call spiking_rules(n,m);
        call neuron_division_rules(n);
        call neuron_budding_rules(n);
}

def spiking_init_conf(n,m)
{
        @mu = in, out;
        @mu += 0,1,2,3;
        @mu += d{i} : 0<=i<=n;
        @mu += Cx{i} : 1<=i<=n;
        @mu += Cx{i,0} : 1<=i<=n;
        @mu += Cx{i,1} : 1<=i<=n;
        @ms(d{0}) = a;
        @ms(0) = a;
        @ms(2) = a;
        @ms(3) = a;
        @ms(d{1}) = a*6;

        @marcs  = (d{i},d{i+1}):0<=i<=n-1;
        @marcs += (d{n},d{1});
        @marcs += (in,Cx{i}):1<=i<=n;
        @marcs += (d{i},Cx{i}):1<=i<=n;
        @marcs += (Cx{i},Cx{i,0}):1<=i<=n;
        @marcs += (Cx{i},Cx{i,1}):1<=i<=n;
        @marcs += ({i+1},{i}):0<=i<=2;
        @marcs += (1,2);
        @marcs += (0,out);

        @mdict = (Cx{i,1},t{i}):1<=i<=n;
        @mdict+= (Cx{i,0},f{i}):1<=i<=n;

        @min = in;

        @minst+= ((2*n+j)+(n*(i-1)),val{i,j}):1<=i<=m, 1<=j<=n;

        @mout = out;
}


def spiking_rules(n,m)
{
        [a --> a]'in;
        [a*2 --> a*2]'in;
        [a --> a]'d{0} :: 2*n+n*m;
        [a*4 --> a*4]'d{i} : 1<=i<=n;
        [a*5 --> #]'d{1};
        [a*6 --> a*4]'d{1} :: 2*n+1;
        [a --> #]'Cx{i} : 1<=i<=n;
        [a*2 --> #]'Cx{i} : 1<=i<=n;
        [a*4 --> #]'Cx{i} : 1<=i<=n;
        [a*5 --> a*5]'Cx{i} :: n-i : 1<=i<=n;
        [a*6 --> a*6]'Cx{i} :: n-i : 1<=i<=n;
        [a*5 --> a*4]'Cx{i,1} : 1<=i<=n;
        [a*6 --> #]'Cx{i,1} : 1<=i<=n;
        [a*5 --> #]'Cx{i,0} : 1<=i<=n;
        [a*6 --> a*4]'Cx{i,0} : 1<=i<=n;
        [a --> a]'t{i} "(a{4})+" : 1<=i<=n;
        [a --> a]'f{i} "(a{4})+" : 1<=i<=n;
        [a*(4*k-1) --> #]'t{i} : 1<=k<=n,1<=i<=n;
        [a*(4*k-1) --> #]'f{i} : 1<=k<=n,1<=i<=n;
        [a*m --> a*2]'cl;
        [a --> a]'out "(a{2})+";
        [a --> a]'{i} : 1<=i<=2;
        [a*2 --> #]'2;
        [a --> a]'3 :: 2*n-1;
}

def neuron_division_rules(n)
{
        []'0 --> []'t{1} || []'f{1} "a";
        []'t{i} --> []'t{i+1} || []'f{i+1} "a" : 1<=i<=n-1;
        []'f{i} --> []'t{i+1} || []'f{i+1} "a" : 1<=i<=n-1;
}

def neuron_budding_rules(n)
{
        []'t{n} --> []'t{n} / []'cl "a";
        []'f{n} --> []'f{n} / []'cl "a";
}

Files

A first run

• Custom application, defining the needed input and output tables for SAT problem solved with spiking neural P systems.
• Model file, P-Lingua file with the parametrized file specifying the family of P systems for solving the partition problem. The custom interface enable the user to introduce the data corresponding to each different scenario.
• Scenario file, for a specific instance of the problem (that is, a specific graph to set the partition to).

Final results

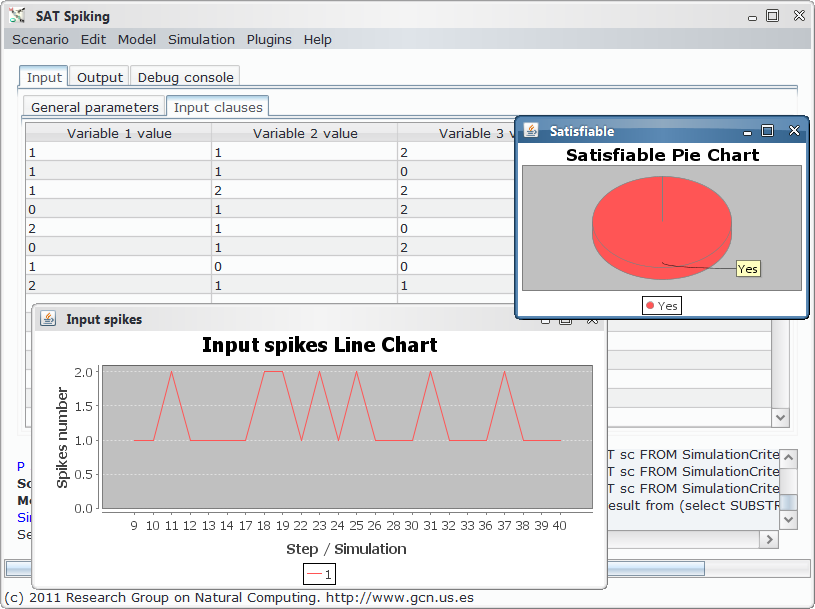
References

[1]	L Pan, Gh. Păun, M.J. Pérez-Jiménez. Spiking neural P systems with neuron division and budding. Science China. Information Sciences, 54, 8 (2011), 1596-1607 (doi:10.1007/s11432-011-4303-y).

[2]

L.F. Macías, I. Pérez-Hurtado, M. García-Quismondo, L. Valencia, M.J. Pérez-Jiménez, A. Riscos. A P-Lingua based simulator for Spiking Neural P systems. Membrane Computing, 12th International Conference, CMC 2011, Fontainebleau, France, August 23-26, 2011, Revised Selected Papers. Lecture Notes in Computer Science, 7184 (2012), 257-281 (doi: 10.1007/978-3-642-28024-5_18).

[3]	L.F. Macías.`Presentation slides <http://cmc12.lacl.fr/media/cmc12/slides/Ramos.pdf>`_ of the paper above, presented in Fontainebleau (Paris, France), Aug. 2011.