SAT - P systems with Symport/Antiport Rules and Membrane Separation Rules¶
Description¶
Well-known problem SAT, solved with P systems with Symport/Antiport Rules and Membrane Separation Rules.
Model in P-Lingua¶
The corresponding P-Lingua file is presented below. In the last function, module_input, several examples are provided. The last one is the one currently active (that is, the only one not commented), which is consistent with the initial lines setting n=6 and m=64.:
/* Note that these lines
are commented */
To change to a different example (that is, another input formula), simply change n and m values, comment the final example and uncomment the lines corresponding to the desired example. Following some explanations are provided to run the parametered version of this model, applicable to any input formula given visually, without altering the code:
@model<infEnv_symport_antiport>
def main()
{
let n = 6;
let m = 64;
call module_alphabet(n,m);
call module_init_conf(n,m);
call module_rules(n,m);
call module_input();
}
def module_alphabet (n,m)
{
@msInfEnv += alpha{i,j,k}, alphap{i,j,k} : 0 <= k <= 1, 1 <= j <= 3*(n-1), 1 <= i <= n-1;
@msInfEnv += beta{j},betap{j},betapp{j},gamma{j},gammap{j},gammapp{j},gammappp{j} : 0 <= j <= 3*(n-1);
@msInfEnv += rho{i,j}, tau{i,j} : 1 <= j <= 3*n-1, 1 <= i <= n;
@msInfEnv += T{i,j},Tp{i,j},F{i,j},Fp{i,j} : i< j <= n, 1 <= i <= n-1;
@msInfEnv += T{i,i},Fp{i,i} : 1 <= i <= n;
@msInfEnv += T{i},F{i} : 1 <= i <= n;
@msInfEnv += A{i},Ap{i},B{i},Bp{i} : 2 <= i <= n + 1;
@msInfEnv += b{i},bp{i},c{i},cp{i} : 2 <= i <= n;
@msInfEnv += v{i} : 2 <= i <= n-1;
@msInfEnv += y{i},a{i},w{i} : 1 <= i <= n-1;
@msInfEnv += z{i} : 1 <= i <= n-2;
@msInfEnv += q{i,j},t{i,j},f{i,j},r{i,j},s{i,j} : i <= j <= n-1, 1 <= i <= n-1;
@msInfEnv += u{i,j} : i <= j <= n-2, 1 <= i <= n-2;
@msInfEnv += e{i,j},_e{i,j} : 1 <= j <= m, 1 <= i <= n;
@msInfEnv += d{i,j,k},_d{i,j,k} : 1 <= k <= n-1, 1 <= j <= m, 1 <= i <= n;
@msInfEnv += f{r} : 1 <= r <= 3*n+2*m;
@msInfEnv += fp{r} : 1 <= r <= 3*n+2*m+1;
@msInfEnv += delta{s,j} : 1 <= j <= 3*n, 0 <= s <= m;
@msInfEnv += E{s} : 0 <= s <= m;
@msInfEnv += S;
}
def module_init_conf(n,m)
{
@mu = [ [[]'2 []'3]'1 ]'environment;
@ms1 += A{i},B{i} : 1 <= i <= n + 1;
@ms1 += T{i,j},F{i,j} : 1 <= j <= n, 1 <= i <= n;
@ms2 += Ap{i},Bp{i} : 2 <= i <= n + 1;
@ms2 += Tp{i,j},Fp{i,j} : i < j <= n, 1 <= i <= n-1;
@ms2 += Fp{i,i} : 1 <= i <= n;
@ms(1) += alpha{i,0,k},alphap{i,0,k} : 0 <= k <= 1, 1 <= i <= n-1;
@ms(1) += rho{i,0},tau{i,0} : 1 <= i <= n;
@ms(1) += beta{0},betap{0},betapp{0},gamma{0},gammap{0},gammapp{0},gammappp{0},sigma{0},sigmap{0};
@ms(1) += c{1},cp{1},b{1},bp{1},v{1},q{1,1}, f{0},yes;
@ms(1) += delta{j,0} : 0 <= j <= m;
@ms(1) += fp{r} : 1 <= r <= 3*n+2*m+1;
@ms(2) += A{1},B{1};
@ms(3) += fp{0},no;
}
def module_rules(n,m)
{
call module_rules_R1(n,m);
call module_rules_R2(n,m);
call module_rules_R3(n,m);
}
def module_rules_R1 (n,m)
{
alpha{i,j+1,k}[alpha{i,j,k}]'1 --> alpha{i,j,k}[alpha{i,j+1,k}]'1 : 0<=j<=2, 0 <= k <= 1, 1 <= i <= n-1;
alphap{i,j+1,k}[alphap{i,j,k}]'1 --> alphap{i,j,k}[alphap{i,j+1,k}]'1 : 0<=j<=2, 0 <= k <= 1, 1 <= i <= n-1;
alpha{i,3*r+1,0},F{i,r+1}[alpha{i,3*r,0}]'1 --> alpha{i,3*r,0}[alpha{i,3*r+1,0},F{i,r+1}]'1 : 1 <= i <= r, 1 <= r <= n - 2;
alpha{i,3*r+1,1},T{i,r+1}[alpha{i,3*r,1}]'1 --> alpha{i,3*r,1}[alpha{i,3*r+1,1},T{i,r+1}]'1 : 1 <= i <= r, 1 <= r <= n - 2;
alphap{i,3*r+1,0},Fp{i,r+1}[alphap{i,3*r,0}]'1 --> alphap{i,3*r,0}[alphap{i,3*r+1,0},Fp{i,r+1}]'1 : 1 <= i <= r, 1 <= r <= n - 2;
alphap{i,3*r+1,1},Tp{i,r+1}[alphap{i,3*r,1}]'1 --> alphap{i,3*r,1}[alphap{i,3*r+1,1},Tp{i,r+1}]'1 : 1 <= i <= r, 1 <= r <= n - 2;
alpha{i,3*r+1,k}[alpha{i,3*r,k}]'1 --> alpha{i,3*r,k}[alpha{i,3*r+1,k}]'1 : 0 <= k <= 1, r + 1 <= i <= n - 1 , 1 <= r <= n - 2;
alphap{i,3*r+1,k}[alphap{i,3*r,k}]'1 --> alphap{i,3*r,k}[alphap{i,3*r+1,k}]'1 : 0 <= k <= 1, r + 1 <= i <= n - 1 , 1 <= r <= n - 2;
alpha{i,3*r+2,k}[alpha{i,3*r+1,k}]'1 --> alpha{i,3*r+1,k}[alpha{i,3*r+2,k}]'1 : 0 <= k <= 1, 1 <= i <= n - 1, 1 <= r <= n - 2;
alphap{i,3*r+2,k}[alphap{i,3*r+1,k}]'1 --> alphap{i,3*r+1,k}[alphap{i,3*r+2,k}]'1 : 0 <= k <= 1, 1 <= i <= n - 1, 1 <= r <= n - 2;
alpha{i,3*r+3,k}*2[alpha{i,3*r+2,k}]'1 --> alpha{i,3*r+2,k}[alpha{i,3*r+3,k}*2]'1 : 0 <= k <= 1, 1 <= i <= n - 1, 1 <= r <= n - 2;
alphap{i,3*r+3,k}*2[alphap{i,3*r+2,k}]'1 --> alphap{i,3*r+2,k}[alphap{i,3*r+3,k}*2]'1 : 1 <= i <= n - 1, 1 <= r <= n - 2, 0 <= k <= 1;
F{i,n}[alpha{i,3*(n-1),0}]'1 --> alpha{i,3*(n-1),0}[F{i,n}]'1 : 1 <= i <= n - 1;
T{i,n}[alpha{i,3*(n-1),1}]'1 --> alpha{i,3*(n-1),1}[T{i,n}]'1 : 1 <= i <= n - 1;
Fp{i,n}[alphap{i,3*(n-1),0}]'1 --> alphap{i,3*(n-1),0}[Fp{i,n}]'1 : 1 <= i <= n - 1;
Tp{i,n}[alphap{i,3*(n-1),1}]'1 --> alphap{i,3*(n-1),1}[Tp{i,n}]'1 : 1 <= i <= n - 1;
/* First group of "beta rules" */
beta{3*r+1},B{r+2}[beta{3*r}]'1 --> beta{3*r}[beta{3*r+1},B{r+2}]'1 : 0 <= r <= n - 3;
betap{3*r+1},Bp{r+2}[betap{3*r}]'1 --> betap{3*r}[betap{3*r+1},Bp{r+2}]'1 : 0 <= r <= n - 3;
betapp{3*r+1},S[betapp{3*r}]'1 --> betapp{3*r}[betapp{3*r+1},S]'1 : 0 <= r <= n - 3;
beta{3*r+2}[beta{3*r+1}]'1 --> beta{3*r+1}[beta{3*r+2}]'1 : 0 <= r <= n - 3;
betap{3*r+2}[betap{3*r+1}]'1 --> betap{3*r+1}[betap{3*r+2}]'1 : 0 <= r <= n - 3;
betapp{3*r+2}[betapp{3*r+1}]'1 --> betapp{3*r+1}[betapp{3*r+2}]'1 : 0 <= r <= n - 3;
beta{3*r+3}*2[beta{3*r+2}]'1 --> beta{3*r+2}[beta{3*r+3}*2]'1 : 0 <= r <= n - 3;
betap{3*r+3}*2[betap{3*r+2}]'1 --> betap{3*r+2}[betap{3*r+3}*2]'1 : 0 <= r <= n - 3;
betapp{3*r+3}*2[betapp{3*r+2}]'1 --> betapp{3*r+2}[betapp{3*r+3}*2]'1 : 0 <= r <= n - 3;
/* Second group of "beta rules" */
beta{3*(n-2)+1},B{n}[beta{3*(n-2)}]'1 --> beta{3*(n-2)}[beta{3*(n-2)+1},B{n}]'1;
betap{3*(n-2)+1},Bp{n}[betap{3*(n-2)}]'1 --> betap{3*(n-2)}[betap{3*(n-2)+1},Bp{n}]'1;
betapp{3*(n-2)+1},S[betapp{3*(n-2)}]'1 --> betapp{3*(n-2)}[betapp{3*(n-2)+1},S]'1;
beta{3*(n-2)+2}[beta{3*(n-2)+1}]'1 --> beta{3*(n-2)+1}[beta{3*(n-2)+2}]'1;
betap{3*(n-2)+2}[betap{3*(n-2)+1}]'1 --> betap{3*(n-2)+1}[betap{3*(n-2)+2}]'1;
betapp{3*(n-2)+2}[betapp{3*(n-2)+1}]'1 --> betapp{3*(n-2)+1}[betapp{3*(n-2)+2}]'1;
beta{3*(n-2)+3}*2[beta{3*(n-2)+2}]'1 --> beta{3*(n-2)+2}[beta{3*(n-2)+3}*2]'1;
betap{3*(n-2)+3}*2[betap{3*(n-2)+2}]'1 --> betap{3*(n-2)+2}[betap{3*(n-2)+3}*2]'1;
betapp{3*(n-2)+3}*2[betapp{3*(n-2)+2}]'1 --> betapp{3*(n-2)+2}[betapp{3*(n-2)+3}*2]'1;
/* Third group of "beta rules" */
B{n+1}[beta{3*(n-1)}]'1 --> beta{3*(n-1)}[B{n+1}]'1;
Bp{n+1}[betap{3*(n-1)}]'1 --> betap{3*(n-1)}[Bp{n+1}]'1;
S[betapp{3*(n-1)}]'1 --> betapp{3*(n-1)}[S]'1;
/* First group of "gamma rules" */
gamma{3*r+1},T{r+1,r+1}[gamma{3*r}]'1 --> gamma{3*r}[gamma{3*r+1},T{r+1,r+1}]'1 : 0 <= r <= n - 3;
gammap{3*r+1},Fp{r+1,r+1}[gammap{3*r}]'1 --> gammap{3*r}[gammap{3*r+1},Fp{r+1,r+1}]'1 : 0 <= r <= n - 3;
gammapp{3*r+1},A{r+2}[gammapp{3*r}]'1 --> gammapp{3*r}[gammapp{3*r+1},A{r+2}]'1 : 0 <= r <= n - 3;
gammappp{3*r+1},Ap{r+2}[gammappp{3*r}]'1 --> gammappp{3*r}[gammappp{3*r+1},Ap{r+2}]'1 : 0 <= r <= n - 3;
gamma{3*r+2}[gamma{3*r+1}]'1 --> gamma{3*r+1}[gamma{3*r+2}]'1 : 0 <= r <= n - 3;
gammap{3*r+2}[gammap{3*r+1}]'1 --> gammap{3*r+1}[gammap{3*r+2}]'1 : 0 <= r <= n - 3;
gammapp{3*r+2}[gammapp{3*r+1}]'1 --> gammapp{3*r+1}[gammapp{3*r+2}]'1 : 0 <= r <= n - 3;
gammappp{3*r+2}[gammappp{3*r+1}]'1 --> gammappp{3*r+1}[gammappp{3*r+2}]'1 : 0 <= r <= n - 3;
gamma{3*r+3}*2[gamma{3*r+2}]'1 --> gamma{3*r+2}[gamma{3*r+3}*2]'1 : 0 <= r <= n - 3;
gammap{3*r+3}*2[gammap{3*r+2}]'1 --> gammap{3*r+2}[gammap{3*r+3}*2]'1 : 0 <= r <= n - 3;
gammapp{3*r+3}*2[gammapp{3*r+2}]'1 --> gammapp{3*r+2}[gammapp{3*r+3}*2]'1 : 0 <= r <= n - 3;
gammappp{3*r+3}*2[gammappp{3*r+2}]'1 --> gammappp{3*r+2}[gammappp{3*r+3}*2]'1 : 0 <= r <= n - 3;
/* Second group of "gamma rules" */
gamma{3*(n-2)+1},T{n-1,n-1}[gamma{3*(n-2)}]'1 --> gamma{3*(n-2)}[gamma{3*(n-2)+1},T{n-1,n-1}]'1;
gammap{3*(n-2)+1},Fp{n-1,n-1}[gammap{3*(n-2)}]'1 --> gammap{3*(n-2)}[gammap{3*(n-2)+1},Fp{n-1,n-1}]'1;
gammapp{3*(n-2)+1},A{n}[gammapp{3*(n-2)}]'1 --> gammapp{3*(n-2)}[gammapp{3*(n-2)+1},A{n}]'1;
gammappp{3*(n-2)+1},Ap{n}[gammappp{3*(n-2)}]'1 --> gammappp{3*(n-2)}[gammappp{3*(n-2)+1},Ap{n}]'1;
gamma{3*(n-2)+2}[gamma{3*(n-2)+1}]'1 --> gamma{3*(n-2)+1}[gamma{3*(n-2)+2}]'1;
gammap{3*(n-2)+2}[gammap{3*(n-2)+1}]'1 --> gammap{3*(n-2)+1}[gammap{3*(n-2)+2}]'1;
gammapp{3*(n-2)+2}[gammapp{3*(n-2)+1}]'1 --> gammapp{3*(n-2)+1}[gammapp{3*(n-2)+2}]'1;
gammappp{3*(n-2)+2}[gammappp{3*(n-2)+1}]'1 --> gammappp{3*(n-2)+1}[gammappp{3*(n-2)+2}]'1;
gamma{3*(n-2)+3}*2[gamma{3*(n-2)+2}]'1 --> gamma{3*(n-2)+2}[gamma{3*(n-2)+3}*2]'1;
gammap{3*(n-2)+3}*2[gammap{3*(n-2)+2}]'1 --> gammap{3*(n-2)+2}[gammap{3*(n-2)+3}*2]'1;
gammapp{3*(n-2)+3}*2[gammapp{3*(n-2)+2}]'1 --> gammapp{3*(n-2)+2}[gammapp{3*(n-2)+3}*2]'1;
gammappp{3*(n-2)+3}*2[gammappp{3*(n-2)+2}]'1 --> gammappp{3*(n-2)+2}[gammappp{3*(n-2)+3}*2]'1;
/* Third group of "gamma rules" */
T{n,n}[gamma{3*(n-1)}]'1 --> gamma{3*(n-1)}[T{n,n}]'1;
Fp{n,n}[gammap{3*(n-1)}]'1 --> gammap{3*(n-1)}[Fp{n,n}]'1;
A{n+1}[gammapp{3*(n-1)}]'1 --> gammapp{3*(n-1)}[A{n+1}]'1;
Ap{n+1}[gammappp{3*(n-1)}]'1 --> gammappp{3*(n-1)}[Ap{n+1}]'1;
/* First group of "rho-tau rules"*/
rho{i,j+1}[rho{i,j}]'1 --> rho{i,j}[rho{i,j+1}]'1 : 0<=j<=2, 1 <= i <= n;
tau{i,j+1}[tau{i,j}]'1 --> tau{i,j}[tau{i,j+1}]'1 : 0<=j<=2, 1 <= i <= n;
/* Second group of "rho-tau rules"*/
rho{i,3*r+1}[rho{i,3*r}]'1 --> rho{i,3*r}[rho{i,3*r+1}]'1 : 1 <= r <= n - 2, 1 <= i <= n;
tau{i,3*r+1}[tau{i,3*r}]'1 --> tau{i,3*r}[tau{i,3*r+1}]'1 : 1 <= r <= n - 2, 1 <= i <= n;
rho{i,3*r+2}*2[rho{i,3*r+1}]'1 --> rho{i,3*r+1}[rho{i,3*r+2}*2]'1 : 1 <= r <= n - 2, 1 <= i <= n;
tau{i,3*r+2}*2[tau{i,3*r+1}]'1 --> tau{i,3*r+1}[tau{i,3*r+2}*2]'1 : 1 <= r <= n - 2, 1 <= i <= n;
rho{i,3*r+3}[rho{i,3*r+2}]'1 --> rho{i,3*r+2}[rho{i,3*r+3}]'1 : 1 <= r <= n - 2, 1 <= i <= n;
tau{i,3*r+3}[tau{i,3*r+2}]'1 --> tau{i,3*r+2}[tau{i,3*r+3}]'1 : 1 <= r <= n - 2, 1 <= i <= n;
/* Second group of "rho-tau rules"*/
rho{i,3*(n-1)+1}[rho{i,3*(n-1)}]'1 --> rho{i,3*(n-1)}[rho{i,3*(n-1)+1}]'1 : 1 <= i <= n;
tau{i,3*(n-1)+1}[tau{i,3*(n-1)}]'1 --> tau{i,3*(n-1)}[tau{i,3*(n-1)+1}]'1 : 1 <= i <= n;
rho{i,3*(n-1)+2}*2[rho{i,3*(n-1)+1}]'1 --> rho{i,3*(n-1)+1}[rho{i,3*(n-1)+2}*2]'1 : 1 <= i <= n;
tau{i,3*(n-1)+2}*2[tau{i,3*(n-1)+1}]'1 --> tau{i,3*(n-1)+1}[tau{i,3*(n-1)+2}*2]'1 : 1 <= i <= n;
T{i}[rho{i,3*(n-1)+2}]'1 --> rho{i,3*(n-1)+2}[T{i}]'1 : 1 <= i <= n;
F{i}[tau{i,3*(n-1)+2}]'1 --> tau{i,3*(n-1)+2}[F{i}]'1 : 1 <= i <= n;
a{i}[A{i}]'1 --> A{i}[a{i}]'1 : 1 <= i <= n - 1;
a{i}[Ap{i}]'1 --> Ap{i}[a{i}]'1 : 1 <= i <= n - 1;
a{i}[B{i}]'1 --> B{i}[a{i}]'1 : 1 <= i <= n - 1;
a{i}[Bp{i}]'1 --> Bp{i}[a{i}]'1 : 1 <= i <= n - 1;
z{i},w{i}[y{i}]'1 --> y{i}[z{i},w{i}]'1 : 1 <= i <= n - 2;
w{n-1}[y{n-1}]'1 --> y{n-1}[w{n-1}]'1;
c{i+1},cp{i+1}[w{i}]'1 --> w{i}[c{i+1},cp{i+1}]'1 : 1 <= i <= n - 1;
v{i+1}[z{i}]'1 --> z{i}[v{i+1}]'1 : 1 <= i <= n - 2;
y{i}*2[v{i}]'1 --> v{i}[y{i}*2]'1 : 1 <= i <= n - 1;
b{i+1},bp{i+1}[a{i}]'1 --> a{i}[b{i+1},bp{i+1}]'1 : 1 <= i <= n - 1;
r{1,1}[q{1,1}]'1 --> q{1,1}[r{1,1}]'1;
r{i,j}*2[q{i,j}]'1 --> q{i,j}[r{i,j}*2]'1 : i <= j <= n - 1, 1 <= i <= n - 1;
s{i,j},u{i,j}[r{i,j}]'1 --> r{i,j}[s{i,j},u{i,j}]'1 : i <= j <= n - 2, 1 <= i <= n - 2;
s{i,n-1}[r{i,n-1}]'1 --> r{i,n-1}[s{i,n-1}]'1 : 1 <= i <= n - 1;
t{i,j},f{i,j}[s{i,j}]'1 --> s{i,j}[t{i,j},f{i,j}]'1 : i <= j <= n - 1, 1 <= i <= n - 1;
q{1,j+1},q{2,j+1}[u{1,j}]'1 --> u{1,j}[q{1,j+1},q{2,j+1}]'1 : 1 <= j <= n - 2;
q{i+1,j+1}[u{i,j}]'1 --> u{i,j}[q{i+1,j+1}]'1 : 2 <= i <= j, 2 <= j <= n - 2;
[T{i,j},t{i,j}]'1 --> T{i,j},t{i,j}[]'1 : 1 <= i <= j,1 <= j <= n;
[Tp{i,j},t{i,j}]'1 --> Tp{i,j},t{i,j}[]'1 : 1 <= i <= j,1 <= j <= n;
[F{i,j},f{i,j}]'1 --> F{i,j},f{i,j}[]'1 : 1 <= i <= j,1 <= j <= n;
[Fp{i,j},f{i,j}]'1 --> Fp{i,j},f{i,j}[]'1 : 1 <= i <= j,1 <= j <= n;
d{i,j,1}*2[x{i,j}]'1 --> x{i,j}[d{i,j,1}*2]'1 : 1 <= j <= m, 1 <= i <= n;
_d{i,j,1}*2[_x{i,j}]'1 --> _x{i,j}[_d{i,j,1}*2]'1 : 1 <= j <= m, 1 <= i <= n;
d{i,j,k+1}*2[d{i,j,k}]'1 --> d{i,j,k}[d{i,j,k+1}*2]'1 : 1 <= k <= n-2, 1 <= j <= m, 1 <= i <= n;
_d{i,j,k+1}*2[_d{i,j,k}]'1 --> _d{i,j,k}[_d{i,j,k+1}*2]'1 : 1 <= k <= n-2, 1 <= j <= m, 1 <= i <= n;
e{i,j}[d{i,j,n-1}]'1 --> d{i,j,n-1}[e{i,j}]'1 : 1 <= j <= m, 1 <= i <= n;
_e{i,j}[_d{i,j,n-1}]'1 --> _d{i,j,n-1}[_e{i,j}]'1 : 1 <= j <= m, 1 <= i <= n;
[E{0},f{3*n+2*m},yes]'1 --> E{0},f{3*n+2*m},yes[]'1;
[f{3*n+2*m},no]'1 --> f{3*n+2*m},no[]'1;
delta{j,3*r+1}[delta{j,3*r}]'1 --> delta{j,3*r}[delta{j,3*r+1}]'1 : 0 <= r <= n - 1, 0 <= j <= m;
delta{j,3*r+2}*2[delta{j,3*r+1}]'1 --> delta{j,3*r+1}[delta{j,3*r+2}*2]'1 : 0 <= r <= n - 1, 0 <= j <= m;
delta{j,3*r+3}[delta{j,3*r+2}]'1 --> delta{j,3*r+2}[delta{j,3*r+3}]'1 : 0 <= r <= n - 2, 0 <= j <= m;
E{1}[delta{1,3*(n-1)+2}]'1 --> delta{1,3*(n-1)+2}[E{1}]'1;
delta{j,3*(n-1)+3}[delta{j,3*(n-1)+2}]'1 --> delta{j,3*(n-1)+2}[delta{j,3*(n-1)+3}]'1 : 0 <= j <= m, j <> 1;
E{j}[delta{j,3*n}]'1 --> delta{j,3*n}[E{j}]'1 : 0 <= j <= m, j <> 1;
f{i+1}[f{i}]'1 --> f{i}[f{i+1}]'1 : 0 <= i <= 3*n + 2*m - 1;
/* garbage rules */
[t{i,k},T{i,k}]'1 --> t{i,k},T{i,k}[]'1 : 1 <= i < k, 2 <= k <= n;
[t{i,k},Tp{i,k}]'1 --> t{i,k},Tp{i,k}[]'1 : 1 <= i < k, 2 <= k <= n;
[f{i,k},F{i,k}]'1 --> f{i,k},F{i,k}[]'1 : 1 <= i < k, 2 <= k <= n;
[f{i,k},Fp{i,k}]'1 --> f{i,k},Fp{i,k}[]'1 : 1 <= i < k, 2 <= k <= n;
[t{i,i},T{i,i}]'1 --> t{i,i},T{i,i}[]'1 : 1 <= i <= n;
[f{i,i},Fp{i,i}]'1 --> f{i,i},Fp{i,i}[]'1 : 1 <= i <= n;
[b{k},B{k+1}]'1 --> b{k},B{k+1}[]'1 : n - 1 <= k <= n;
[bp{k},Bp{k+1}]'1 --> bp{k},Bp{k+1}[]'1 : n - 1 <= k <= n;
[cp{k},Ap{k+1}]'1 --> cp{k},Ap{k+1}[]'1 : n - 1 <= k <= n;
[c{k},A{k+1}]'1 --> c{k},A{k+1}[]'1 : n - 1 <= k <= n;
}
def module_rules_R2 (n,m)
{
[S]'2 --> []'2[]'2;
c{i},cp{i}[A{i}]'2 --> A{i}[c{i},cp{i}]'2 : 1<= i <= n;
c{i},cp{i}[Ap{i}]'2 --> Ap{i}[c{i},cp{i}]'2 : 1<= i <= n;
b{i},bp{i}[B{i}]'2 --> B{i}[b{i},bp{i}]'2 : 1<= i <= n;
b{i},bp{i}[Bp{i}]'2 --> Bp{i}[b{i},bp{i}]'2 : 1<= i <= n;
B{i+1},S[b{i}]'2 --> b{i}[B{i+1},S]'2 : 1<= i <= n;
Bp{i+1}[bp{i}]'2 --> bp{i}[Bp{i+1}]'2 : 1<= i <= n;
T{i,i},A{i+1}[c{i}]'2 --> c{i}[T{i,i},A{i+1}]'2 : 1<= i <= n;
Fp{i,i},Ap{i+1}[cp{i}]'2 --> cp{i}[Fp{i,i},Ap{i+1}]'2 : 1<= i <= n;
E{1}[B{n+1}]'2 --> B{n+1}[E{1}]'2;
E{1}[Bp{n+1}]'2 --> Bp{n+1}[E{1}]'2;
E{0}[A{n+1}]'2 --> A{n+1}[E{0}]'2;
E{0}[Ap{n+1}]'2 --> Ap{n+1}[E{0}]'2;
t{i,j}[T{i,j}]'2 --> T{i,j}[t{i,j}]'2 : 1 <= i <= j,1 <= j <= n;
t{i,j}[Tp{i,j}]'2 --> Tp{i,j}[t{i,j}]'2 : 1 <= i <= j,1 <= j <= n;
f{i,j}[F{i,j}]'2 --> F{i,j}[f{i,j}]'2 : 1 <= i <= j,1 <= j <= n;
f{i,j}[Fp{i,j}]'2 --> Fp{i,j}[f{i,j}]'2 : 1 <= i <= j,1 <= j <= n;
T{i,j+1},Tp{i,j+1}[t{i,j}]'2 --> t{i,j}[T{i,j+1},Tp{i,j+1}]'2 : 1 <= i <= j,1 <= j <= n-1;
F{i,j+1},Fp{i,j+1}[f{i,j}]'2 --> f{i,j}[F{i,j+1},Fp{i,j+1}]'2 : 1 <= i <= j,1 <= j <= n-1;
T{i}[T{i,n}]'2 --> T{i,n}[T{i}]'2 : 1 <= i <= n;
T{i}[Tp{i,n}]'2 --> Tp{i,n}[T{i}]'2 : 1 <= i <= n;
F{i}[F{i,n}]'2 --> F{i,n}[F{i}]'2 : 1 <= i <= n;
F{i}[Fp{i,n}]'2 --> Fp{i,n}[F{i}]'2 : 1 <= i <= n;
e{i,j}[E{j},T{i}]'2 --> E{j},T{i}[e{i,j}]'2 : 1 <= j <= m, 1 <= i <= n;
_e{i,j}[E{j},F{i}]'2 --> E{j},F{i}[_e{i,j}]'2 : 1 <= j <= m, 1 <= i <= n;
E{j+1},T{i}[e{i,j}]'2 --> e{i,j}[E{j+1},T{i}]'2 : 1 <= j <= m - 1, 1 <= i <= n;
E{j+1},F{i}[_e{i,j}]'2 --> _e{i,j}[E{j+1},F{i}]'2 : 1 <= j <= m - 1, 1 <= i <= n;
[e{i,m},E{0}]'2 --> e{i,m},E{0}[]'2 : 1 <= i <= n;
[_e{i,m},E{0}]'2 --> _e{i,m},E{0}[]'2 : 1 <= i <= n;
}
def module_rules_R3 (n,m)
{
/* R3 */
fp{r+1}[fp{r}]'3 --> fp{r}[fp{r+1}]'3 : 0 <= r <= 3*n+2*m;
[fp{3*n+2*m+1},no]'3 --> fp{3*n+2*m+1},no[]'3;
}
def module_input ()
{
/* Ok. n=4, p=3 (yes) */
/*@ms(1) += x{1,1},x{2,1},x{3,1},_x{4,1};
@ms(1) += x{1,2},_x{2,2},x{3,2},x{4,2};
@ms(1) += _x{1,3},x{2,3},x{3,3},x{4,3};*/
/* Ok. n=4, p=6 (yes) */
/*@ms(1) += _x{2,1},x{3,1},x{4,1};
@ms(1) += x{1,2},_x{2,2},_x{4,2};
@ms(1) += _x{2,3},x{4,3};
@ms(1) += x{1,4},x{3,4};
@ms(1) += _x{1,5},x{2,5};
@ms(1) += x{1,6},_x{2,6},_x{3,6},_x{4,6};*/
/* Ok. n=4, p=7 (no) */
/*@ms(1) += _x{2,1},x{3,1},x{4,1};
@ms(1) += x{1,2},_x{2,2},_x{4,2};
@ms(1) += _x{2,3},x{4,3};
@ms(1) += x{1,4},x{3,4};
@ms(1) += _x{1,5},x{2,5};
@ms(1) += _x{1,6},_x{4,6};
@ms(1) += x{1,7},x{2,7},_x{3,7};*/
/* Ok. n=4, p=6 (no) */
/*@ms(3) += x{1,1};
@ms(3) += x{2,2};
@ms(3) += _x{1,3},_x{2,3};
@ms(3) += x{3,4};
@ms(3) += x{4,5};
@ms(3) += _x{3,6},_x{4,6};*/
/* Ok. n=5, p=32 (no) */
/*@ms(3) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(3) += x{1,2},x{2,2},x{3,2},x{4,2},_x{5,2};
@ms(3) += x{1,3},x{2,3},x{3,3},_x{4,3},x{5,3};
@ms(3) += x{1,4},x{2,4},x{3,4},_x{4,4},_x{5,4};
@ms(3) += x{1,5},x{2,5},_x{3,5},x{4,5},x{5,5};
@ms(3) += x{1,6},x{2,6},_x{3,6},x{4,6},_x{5,6};
@ms(3) += x{1,7},x{2,7},_x{3,7},_x{4,7},x{5,7};
@ms(3) += x{1,8},x{2,8},_x{3,8},_x{4,8},_x{5,8};
@ms(3) += x{1,9},_x{2,9},x{3,9},x{4,9},x{5,9};
@ms(3) += x{1,10},_x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(3) += x{1,11},_x{2,11},x{3,11},_x{4,11},x{5,11};
@ms(3) += x{1,12},_x{2,12},x{3,12},_x{4,12},_x{5,12};
@ms(3) += x{1,13},_x{2,13},_x{3,13},x{4,13},x{5,13};
@ms(3) += x{1,14},_x{2,14},_x{3,14},x{4,14},_x{5,14};
@ms(3) += x{1,15},_x{2,15},_x{3,15},_x{4,15},x{5,15};
@ms(3) += x{1,16},_x{2,16},_x{3,16},_x{4,16},_x{5,16};
@ms(3) += _x{1,17},x{2,17},x{3,17},x{4,17},x{5,17};
@ms(3) += _x{1,18},x{2,18},x{3,18},x{4,18},_x{5,18};
@ms(3) += _x{1,19},x{2,19},x{3,19},_x{4,19},x{5,19};
@ms(3) += _x{1,20},x{2,20},x{3,20},_x{4,20},_x{5,20};
@ms(3) += _x{1,21},x{2,21},_x{3,21},x{4,21},x{5,21};
@ms(3) += _x{1,22},x{2,22},_x{3,22},x{4,22},_x{5,22};
@ms(3) += _x{1,23},x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(3) += _x{1,24},x{2,24},_x{3,24},_x{4,24},_x{5,24};
@ms(3) += _x{1,25},_x{2,25},x{3,25},x{4,25},x{5,25};
@ms(3) += _x{1,26},_x{2,26},x{3,26},x{4,26},_x{5,26};
@ms(3) += _x{1,27},_x{2,27},x{3,27},_x{4,27},x{5,27};
@ms(3) += _x{1,28},_x{2,28},x{3,28},_x{4,28},_x{5,28};
@ms(3) += _x{1,29},_x{2,29},_x{3,29},x{4,29},x{5,29};
@ms(3) += _x{1,30},_x{2,30},_x{3,30},x{4,30},_x{5,30};
@ms(3) += _x{1,31},_x{2,31},_x{3,31},_x{4,31},x{5,31};
@ms(3) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32};*/
/* Ok. n=5, p=41 (no) */
/*@ms(3) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(3) += x{1,2},x{2,2},x{3,2},x{4,2},_x{5,2};
@ms(3) += x{1,3},x{2,3},x{3,3},_x{4,3},x{5,3};
@ms(3) += x{1,4},x{2,4},x{3,4},_x{4,4},_x{5,4};
@ms(3) += x{1,5},x{2,5},_x{3,5},x{4,5},x{5,5};
@ms(3) += x{1,6},x{2,6},_x{3,6},x{4,6},_x{5,6};
@ms(3) += x{1,7},x{2,7},_x{3,7},_x{4,7},x{5,7};
@ms(3) += x{1,8},x{2,8},_x{3,8},_x{4,8},_x{5,8};
@ms(3) += x{1,9},_x{2,9},x{3,9},x{4,9},x{5,9};
@ms(3) += x{1,10},_x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(3) += x{1,11},_x{2,11},x{3,11},_x{4,11},x{5,11};
@ms(3) += x{1,12},_x{2,12},x{3,12},_x{4,12},_x{5,12};
@ms(3) += x{1,13},_x{2,13},_x{3,13},x{4,13},x{5,13};
@ms(3) += x{1,14},_x{2,14},_x{3,14},x{4,14},_x{5,14};
@ms(3) += x{1,15},_x{2,15},_x{3,15},_x{4,15},x{5,15};
@ms(3) += x{1,16},_x{2,16},_x{3,16},_x{4,16},_x{5,16};
@ms(3) += _x{1,17},x{2,17},x{3,17},x{4,17},x{5,17};
@ms(3) += _x{1,18},x{2,18},x{3,18},x{4,18},_x{5,18};
@ms(3) += _x{1,19},x{2,19},x{3,19},_x{4,19},x{5,19};
@ms(3) += _x{1,20},x{2,20},x{3,20},_x{4,20},_x{5,20};
@ms(3) += _x{1,21},x{2,21},_x{3,21},x{4,21},x{5,21};
@ms(3) += _x{1,22},x{2,22},_x{3,22},x{4,22},_x{5,22};
@ms(3) += _x{1,23},x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(3) += _x{1,24},x{2,24},_x{3,24},_x{4,24},_x{5,24};
@ms(3) += _x{1,25},_x{2,25},x{3,25},x{4,25},x{5,25};
@ms(3) += _x{1,26},_x{2,26},x{3,26},x{4,26},_x{5,26};
@ms(3) += _x{1,27},_x{2,27},x{3,27},_x{4,27},x{5,27};
@ms(3) += _x{1,28},_x{2,28},x{3,28},_x{4,28},_x{5,28};
@ms(3) += _x{1,29},_x{2,29},_x{3,29},x{4,29},x{5,29};
@ms(3) += _x{1,30},_x{2,30},_x{3,30},x{4,30},_x{5,30};
@ms(3) += _x{1,31},_x{2,31},_x{3,31},_x{4,31},x{5,31};
@ms(3) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32};
@ms(3) += x{1,33},_x{2,33};
@ms(3) += _x{2,34};
@ms(3) += x{2,35},_x{5,35};
@ms(3) += x{2,36},_x{4,36};
@ms(3) += x{3,37},x{4,37};
@ms(3) += _x{5,38};
@ms(3) += x{3,39},_x{5,39};
@ms(3) += x{1,40},_x{4,40};
@ms(3) += x{3,41},_x{4,41};*/
/* Ok. n=5, p=32 (no) */
/*@ms(3) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(3) += x{1,2},x{2,2},x{3,2},x{4,2},_x{5,2};
@ms(3) += x{1,3},x{2,3},x{3,3},_x{4,3},x{5,3};
@ms(3) += x{1,4},x{2,4},x{3,4},_x{4,4},_x{5,4};
@ms(3) += x{1,5},x{2,5},_x{3,5},x{4,5},x{5,5};
@ms(3) += x{1,6},x{2,6},_x{3,6},x{4,6},_x{5,6};
@ms(3) += x{1,7},x{2,7},_x{3,7},_x{4,7},x{5,7};
@ms(3) += x{1,8},x{2,8},_x{3,8},_x{4,8},_x{5,8};
@ms(3) += x{1,9},_x{2,9},x{3,9},x{4,9},x{5,9};
@ms(3) += x{1,10},_x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(3) += x{1,11},_x{2,11},x{3,11},_x{4,11},x{5,11};
@ms(3) += x{1,12},_x{2,12},x{3,12},_x{4,12},_x{5,12};
@ms(3) += x{1,13},_x{2,13},_x{3,13},x{4,13},x{5,13};
@ms(3) += x{1,14},_x{2,14},_x{3,14},x{4,14},_x{5,14};
@ms(3) += x{1,15},_x{2,15},_x{3,15},_x{4,15},x{5,15};
@ms(3) += x{1,16},_x{2,16},_x{3,16},_x{4,16},_x{5,16};
@ms(3) += _x{1,17},x{2,17},x{3,17},x{4,17},x{5,17};
@ms(3) += _x{1,18},x{2,18},x{3,18},x{4,18},_x{5,18};
@ms(3) += _x{1,19},x{2,19},x{3,19},_x{4,19},x{5,19};
@ms(3) += _x{1,20},x{2,20},x{3,20},_x{4,20},_x{5,20};
@ms(3) += _x{1,21},x{2,21},_x{3,21},x{4,21},x{5,21};
@ms(3) += _x{1,22},x{2,22},_x{3,22},x{4,22},_x{5,22};
@ms(3) += _x{1,23},x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(3) += _x{1,24},x{2,24},_x{3,24},_x{4,24},_x{5,24};
@ms(3) += _x{1,25},_x{2,25},x{3,25},x{4,25},x{5,25};
@ms(3) += _x{1,26},_x{2,26},x{3,26},x{4,26},_x{5,26};
@ms(3) += _x{1,27},_x{2,27},x{3,27},_x{4,27},x{5,27};
@ms(3) += _x{1,28},_x{2,28},x{3,28},_x{4,28},_x{5,28};
@ms(3) += _x{1,29},_x{2,29},_x{3,29},x{4,29},x{5,29};
@ms(3) += _x{1,30},_x{2,30},_x{3,30},x{4,30},_x{5,30};
@ms(3) += _x{1,31},_x{2,31},_x{3,31},_x{4,31},x{5,31};
@ms(3) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32};*/
/* Ok. n=5, p=32 (no) */
/*@ms(1) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(1) += _x{1,2},x{2,2},x{3,2},x{4,2},x{5,2};
@ms(1) += x{1,3},_x{2,3},x{3,3},x{4,3},x{5,3};
@ms(1) += x{1,4},x{2,4},_x{3,4},x{4,4},x{5,4};
@ms(1) += x{1,5},x{2,5},x{3,5},_x{4,5},x{5,5};
@ms(1) += x{1,6},x{2,6},x{3,6},x{4,6},_x{5,6};
@ms(1) += _x{1,7},_x{2,7},x{3,7},x{4,7},x{5,7};
@ms(1) += _x{1,8},x{2,8},_x{3,8},x{4,8},x{5,8};
@ms(1) += _x{1,9},x{2,9},x{3,9},_x{4,9},x{5,9};
@ms(1) += _x{1,10},x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(1) += x{1,11},_x{2,11},_x{3,11},x{4,11},x{5,11};
@ms(1) += x{1,12},_x{2,12},x{3,12},_x{4,12},x{5,12};
@ms(1) += x{1,13},_x{2,13},x{3,13},x{4,13},_x{5,13};
@ms(1) += x{1,14},x{2,14},_x{3,14},_x{4,14},x{5,14};
@ms(1) += x{1,15},x{2,15},_x{3,15},x{4,15},_x{5,15};
@ms(1) += x{1,16},x{2,16},x{3,16},_x{4,16},_x{5,16};
@ms(1) += _x{1,17},_x{2,17},_x{3,17},x{4,17},x{5,17};
@ms(1) += _x{1,18},_x{2,18},x{3,18},_x{4,18},x{5,18};
@ms(1) += _x{1,19},_x{2,19},x{3,19},x{4,19},_x{5,19};
@ms(1) += _x{1,20},x{2,20},_x{3,20},_x{4,20},x{5,20};
@ms(1) += _x{1,21},x{2,21},_x{3,21},x{4,21},_x{5,21};
@ms(1) += _x{1,22},x{2,22},x{3,22},_x{4,22},_x{5,22};
@ms(1) += x{1,23},_x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(1) += x{1,24},_x{2,24},_x{3,24},x{4,24},_x{5,24};
@ms(1) += x{1,25},_x{2,25},x{3,25},_x{4,25},_x{5,25};
@ms(1) += x{1,26},x{2,26},_x{3,26},_x{4,26},_x{5,26};
@ms(1) += _x{1,27},_x{2,27},_x{3,27},_x{4,27},x{5,27};
@ms(1) += _x{1,28},_x{2,28},_x{3,28},x{4,28},_x{5,28};
@ms(1) += _x{1,29},_x{2,29},x{3,29},_x{4,29},_x{5,29};
@ms(1) += _x{1,30},x{2,30},_x{3,30},_x{4,30},_x{5,30};
@ms(1) += x{1,31},_x{2,31},_x{3,31},_x{4,31},_x{5,31};
@ms(1) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32};*/
/* 5, 40 (no)*/
/*@ms(3) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(3) += x{1,2},x{2,2},x{3,2},x{4,2},_x{5,2};
@ms(3) += x{1,3},x{2,3},x{3,3},_x{4,3},x{5,3};
@ms(3) += x{1,4},x{2,4},x{3,4},_x{4,4},_x{5,4};
@ms(3) += x{1,5},x{2,5},_x{3,5},x{4,5},x{5,5};
@ms(3) += x{1,6},x{2,6},_x{3,6},x{4,6},_x{5,6};
@ms(3) += x{1,7},x{2,7},_x{3,7},_x{4,7},x{5,7};
@ms(3) += x{1,8},x{2,8},_x{3,8},_x{4,8},_x{5,8};
@ms(3) += x{1,9},_x{2,9},x{3,9},x{4,9},x{5,9};
@ms(3) += x{1,10},_x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(3) += x{1,11},_x{2,11},x{3,11},_x{4,11},x{5,11};
@ms(3) += x{1,12},_x{2,12},x{3,12},_x{4,12},_x{5,12};
@ms(3) += x{1,13},_x{2,13},_x{3,13},x{4,13},x{5,13};
@ms(3) += x{1,14},_x{2,14},_x{3,14},x{4,14},_x{5,14};
@ms(3) += x{1,15},_x{2,15},_x{3,15},_x{4,15},x{5,15};
@ms(3) += x{1,16},_x{2,16},_x{3,16},_x{4,16},_x{5,16};
@ms(3) += _x{1,17},x{2,17},x{3,17},x{4,17},x{5,17};
@ms(3) += _x{1,18},x{2,18},x{3,18},x{4,18},_x{5,18};
@ms(3) += _x{1,19},x{2,19},x{3,19},_x{4,19},x{5,19};
@ms(3) += _x{1,20},x{2,20},x{3,20},_x{4,20},_x{5,20};
@ms(3) += _x{1,21},x{2,21},_x{3,21},x{4,21},x{5,21};
@ms(3) += _x{1,22},x{2,22},_x{3,22},x{4,22},_x{5,22};
@ms(3) += _x{1,23},x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(3) += _x{1,24},x{2,24},_x{3,24},_x{4,24},_x{5,24};
@ms(3) += _x{1,25},_x{2,25},x{3,25},x{4,25},x{5,25};
@ms(3) += _x{1,26},_x{2,26},x{3,26},x{4,26},_x{5,26};
@ms(3) += _x{1,28},_x{2,28},x{3,28},_x{4,28},_x{5,28};
@ms(3) += _x{1,29},_x{2,29},_x{3,29},x{4,29},x{5,29};
@ms(3) += _x{1,30},_x{2,30},_x{3,30},x{4,30},_x{5,30};
@ms(3) += _x{1,31},_x{2,31},_x{3,31},_x{4,31},x{5,31};
@ms(3) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32};
@ms(3) += x{1,33},_x{2,33};
@ms(3) += _x{2,34};
@ms(3) += x{2,35},_x{5,35};
@ms(3) += x{2,36},_x{4,36};
@ms(3) += x{3,37},x{4,37};
@ms(3) += _x{5,38};
@ms(3) += x{3,39},_x{5,39};
@ms(3) += x{1,40},_x{4,40};
@ms(3) += x{3,27},_x{4,27};*/
/* 5, 31 (yes)*/
/*@ms(1) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1};
@ms(1) += x{1,2},x{2,2},x{3,2},x{4,2},_x{5,2};
@ms(1) += x{1,3},x{2,3},x{3,3},_x{4,3},x{5,3};
@ms(1) += x{1,4},x{2,4},x{3,4},_x{4,4},_x{5,4};
@ms(1) += x{1,5},x{2,5},_x{3,5},x{4,5},x{5,5};
@ms(1) += x{1,6},x{2,6},_x{3,6},x{4,6},_x{5,6};
@ms(1) += x{1,7},x{2,7},_x{3,7},_x{4,7},x{5,7};
@ms(1) += x{1,8},x{2,8},_x{3,8},_x{4,8},_x{5,8};
@ms(1) += x{1,9},_x{2,9},x{3,9},x{4,9},x{5,9};
@ms(1) += x{1,10},_x{2,10},x{3,10},x{4,10},_x{5,10};
@ms(1) += x{1,11},_x{2,11},x{3,11},_x{4,11},x{5,11};
@ms(1) += x{1,12},_x{2,12},x{3,12},_x{4,12},_x{5,12};
@ms(1) += x{1,13},_x{2,13},_x{3,13},x{4,13},x{5,13};
@ms(1) += x{1,14},_x{2,14},_x{3,14},x{4,14},_x{5,14};
@ms(1) += x{1,15},_x{2,15},_x{3,15},_x{4,15},x{5,15};
@ms(1) += x{1,16},_x{2,16},_x{3,16},_x{4,16},_x{5,16};
@ms(1) += _x{1,17},x{2,17},x{3,17},x{4,17},x{5,17};
@ms(1) += _x{1,18},x{2,18},x{3,18},x{4,18},_x{5,18};
@ms(1) += _x{1,19},x{2,19},x{3,19},_x{4,19},x{5,19};
@ms(1) += _x{1,20},x{2,20},x{3,20},_x{4,20},_x{5,20};
@ms(1) += _x{1,21},x{2,21},_x{3,21},x{4,21},x{5,21};
@ms(1) += _x{1,22},x{2,22},_x{3,22},x{4,22},_x{5,22};
@ms(1) += _x{1,23},x{2,23},_x{3,23},_x{4,23},x{5,23};
@ms(1) += _x{1,24},x{2,24},_x{3,24},_x{4,24},_x{5,24};
@ms(1) += _x{1,25},_x{2,25},x{3,25},x{4,25},x{5,25};
@ms(1) += _x{1,26},_x{2,26},x{3,26},x{4,26},_x{5,26};
@ms(1) += _x{1,27},_x{2,27},x{3,27},_x{4,27},x{5,27};
@ms(1) += _x{1,28},_x{2,28},x{3,28},_x{4,28},_x{5,28};
@ms(1) += _x{1,29},_x{2,29},_x{3,29},x{4,29},x{5,29};
@ms(1) += _x{1,30},_x{2,30},_x{3,30},x{4,30},_x{5,30};
@ms(1) += _x{1,31},_x{2,31},_x{3,31},_x{4,31},x{5,31};*/
/* 6, 64 (no)*/
@ms(1) += x{1,1},x{2,1},x{3,1},x{4,1},x{5,1},x{6,1};
@ms(1) += _x{1,2},x{2,2},x{3,2},x{4,2},x{5,2},x{6,2};
@ms(1) += x{1,3},_x{2,3},x{3,3},x{4,3},x{5,3},x{6,3};
@ms(1) += x{1,4},x{2,4},_x{3,4},x{4,4},x{5,4},x{6,4};
@ms(1) += x{1,5},x{2,5},x{3,5},_x{4,5},x{5,5},x{6,5};
@ms(1) += x{1,6},x{2,6},x{3,6},x{4,6},_x{5,6},x{6,6};
@ms(1) += _x{1,7},_x{2,7},x{3,7},x{4,7},x{5,7},x{6,7};
@ms(1) += _x{1,8},x{2,8},_x{3,8},x{4,8},x{5,8},x{6,8};
@ms(1) += _x{1,9},x{2,9},x{3,9},_x{4,9},x{5,9},x{6,9};
@ms(1) += _x{1,10},x{2,10},x{3,10},x{4,10},_x{5,10},x{6,10};
@ms(1) += x{1,11},_x{2,11},_x{3,11},x{4,11},x{5,11},x{6,11};
@ms(1) += x{1,12},_x{2,12},x{3,12},_x{4,12},x{5,12},x{6,12};
@ms(1) += x{1,13},_x{2,13},x{3,13},x{4,13},_x{5,13},x{6,13};
@ms(1) += x{1,14},x{2,14},_x{3,14},_x{4,14},x{5,14},x{6,14};
@ms(1) += x{1,15},x{2,15},_x{3,15},x{4,15},_x{5,15},x{6,15};
@ms(1) += x{1,16},x{2,16},x{3,16},_x{4,16},_x{5,16},x{6,16};
@ms(1) += _x{1,17},_x{2,17},_x{3,17},x{4,17},x{5,17},x{6,17};
@ms(1) += _x{1,18},_x{2,18},x{3,18},_x{4,18},x{5,18},x{6,18};
@ms(1) += _x{1,19},_x{2,19},x{3,19},x{4,19},_x{5,19},x{6,19};
@ms(1) += _x{1,20},x{2,20},_x{3,20},_x{4,20},x{5,20},x{6,20};
@ms(1) += _x{1,21},x{2,21},_x{3,21},x{4,21},_x{5,21},x{6,21};
@ms(1) += _x{1,22},x{2,22},x{3,22},_x{4,22},_x{5,22},x{6,22};
@ms(1) += x{1,23},_x{2,23},_x{3,23},_x{4,23},x{5,23},x{6,23};
@ms(1) += x{1,24},_x{2,24},_x{3,24},x{4,24},_x{5,24},x{6,24};
@ms(1) += x{1,25},_x{2,25},x{3,25},_x{4,25},_x{5,25},x{6,25};
@ms(1) += x{1,26},x{2,26},_x{3,26},_x{4,26},_x{5,26},x{6,26};
@ms(1) += _x{1,27},_x{2,27},_x{3,27},_x{4,27},x{5,27},x{6,27};
@ms(1) += _x{1,28},_x{2,28},_x{3,28},x{4,28},_x{5,28},x{6,28};
@ms(1) += _x{1,29},_x{2,29},x{3,29},_x{4,29},_x{5,29},x{6,29};
@ms(1) += _x{1,30},x{2,30},_x{3,30},_x{4,30},_x{5,30},x{6,30};
@ms(1) += x{1,31},_x{2,31},_x{3,31},_x{4,31},_x{5,31},x{6,31};
@ms(1) += _x{1,32},_x{2,32},_x{3,32},_x{4,32},_x{5,32},x{6,32};
@ms(1) += x{1,33},x{2,33},x{3,33},x{4,33},x{5,33},_x{6,33};
@ms(1) += _x{1,34},x{2,34},x{3,34},x{4,34},x{5,34},_x{6,34};
@ms(1) += x{1,35},_x{2,35},x{3,35},x{4,35},x{5,35},_x{6,35};
@ms(1) += x{1,36},x{2,36},_x{3,36},x{4,36},x{5,36},_x{6,36};
@ms(1) += x{1,37},x{2,37},x{3,37},_x{4,37},x{5,37},_x{6,37};
@ms(1) += x{1,38},x{2,38},x{3,38},x{4,38},_x{5,38},_x{6,38};
@ms(1) += _x{1,39},_x{2,39},x{3,39},x{4,39},x{5,39},_x{6,39};
@ms(1) += _x{1,40},x{2,40},_x{3,40},x{4,40},x{5,40},_x{6,40};
@ms(1) += _x{1,41},x{2,41},x{3,41},_x{4,41},x{5,41},_x{6,41};
@ms(1) += _x{1,42},x{2,42},x{3,42},x{4,42},_x{5,42},_x{6,42};
@ms(1) += x{1,43},_x{2,43},_x{3,43},x{4,43},x{5,43},_x{6,43};
@ms(1) += x{1,44},_x{2,44},x{3,44},_x{4,44},x{5,44},_x{6,44};
@ms(1) += x{1,45},_x{2,45},x{3,45},x{4,45},_x{5,45},_x{6,45};
@ms(1) += x{1,46},x{2,46},_x{3,46},_x{4,46},x{5,46},_x{6,46};
@ms(1) += x{1,47},x{2,47},_x{3,47},x{4,47},_x{5,47},_x{6,47};
@ms(1) += x{1,48},x{2,48},x{3,48},_x{4,48},_x{5,48},_x{6,48};
@ms(1) += _x{1,49},_x{2,49},_x{3,49},x{4,49},x{5,49},_x{6,49};
@ms(1) += _x{1,50},_x{2,50},x{3,50},_x{4,50},x{5,50},_x{6,50};
@ms(1) += _x{1,51},_x{2,51},x{3,51},x{4,51},_x{5,51},_x{6,51};
@ms(1) += _x{1,52},x{2,52},_x{3,52},_x{4,52},x{5,52},_x{6,52};
@ms(1) += _x{1,53},x{2,53},_x{3,53},x{4,53},_x{5,53},_x{6,53};
@ms(1) += _x{1,54},x{2,54},x{3,54},_x{4,54},_x{5,54},_x{6,54};
@ms(1) += x{1,55},_x{2,55},_x{3,55},_x{4,55},x{5,55},_x{6,55};
@ms(1) += x{1,56},_x{2,56},_x{3,56},x{4,56},_x{5,56},_x{6,56};
@ms(1) += x{1,57},_x{2,57},x{3,57},_x{4,57},_x{5,57},_x{6,57};
@ms(1) += x{1,58},x{2,58},_x{3,58},_x{4,58},_x{5,58},_x{6,58};
@ms(1) += _x{1,59},_x{2,59},_x{3,59},_x{4,59},x{5,59},_x{6,59};
@ms(1) += _x{1,60},_x{2,60},_x{3,60},x{4,60},_x{5,60},_x{6,60};
@ms(1) += _x{1,61},_x{2,61},x{3,61},_x{4,61},_x{5,61},_x{6,61};
@ms(1) += _x{1,62},x{2,62},_x{3,62},_x{4,62},_x{5,62},_x{6,62};
@ms(1) += x{1,63},_x{2,63},_x{3,63},_x{4,63},_x{5,63},_x{6,63};
@ms(1) += _x{1,64},_x{2,64},_x{3,64},_x{4,64},_x{5,64},_x{6,64};
}
Files¶
- The example does not need input data from any user nor speficic interesting outputs, so it can be run from the general app yet available and pre-loaded in MeCoSim.
- Model file, P-Lingua file with the code above.
- As in the case of the app, no scenario file with specific input is needed, so the general dummy scenario file can also be used.
Adapting a problem to MeCoSim philosophy¶
The previous model solves our problem, in this case SAT, by means of P systems. With P-Lingua, a general-purpose language, parsers and simulators have been provided.
However, the given P-Lingua file includes the definition of our P system as provided for the designer, but it also incorporates the specific values for m (clauses) and n (variables), thus setting a P system inside the family of SAT<m,n>. Besides, the file also includes the specific input for the system (cod(s)) codifying a formula.
Thus, there is a clear separation between the developer of parsers and simulators and the designer of solutions based on P systems, that have in P-Lingua framework the proper tools to forget about developing software tools for the modelling and simulation and can concentrate in designing solutions based on P systems. But there is no separation between designer and end-user, the instantiation of any P system of the family SAT<m,n> requires the manipulation of the same file including the specification of the family, and the same happens if that end user wants to use the solution for solving the problem for a given formula.
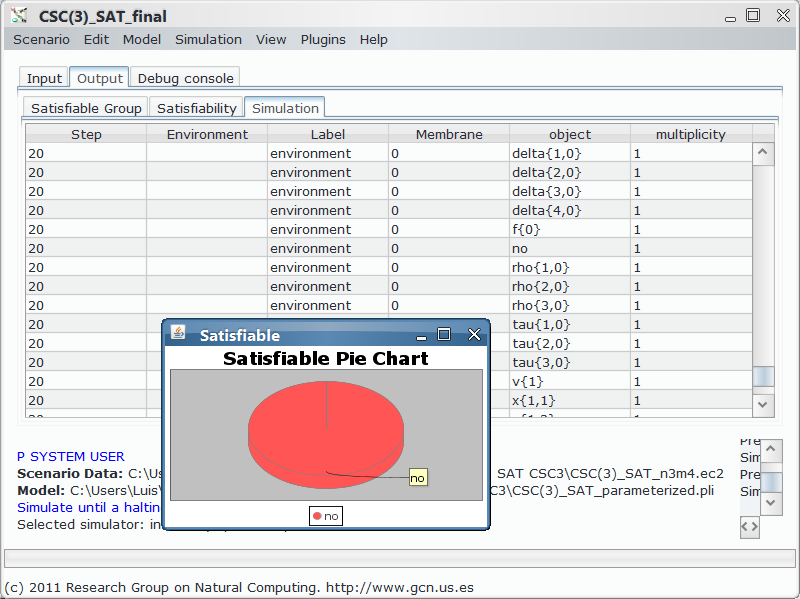
Among the goals of MeCoSim is the clear separation of these roles, so a custom app is provided defining the inputs for introducing the specific instance of the P system and the given formula, along with the outputs adapted to our problem, thus focusing the attention in solving the problem beyond the meta-analysis of the P system, that is interesting for the designer but probably not for a person trying to know the satisfiability of the P system.
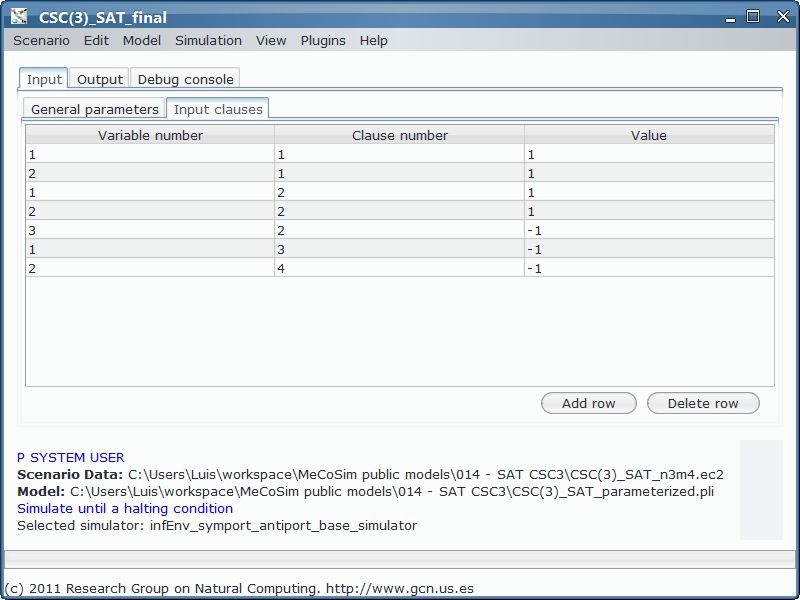
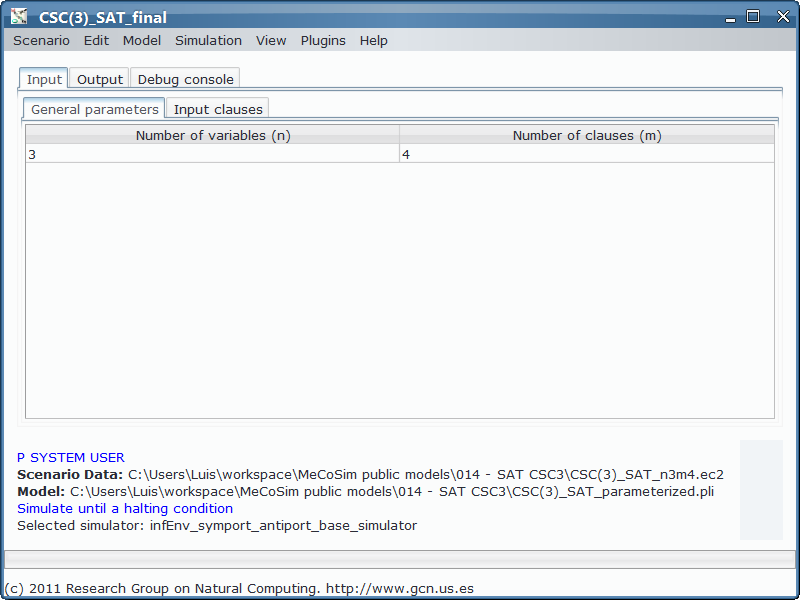
Now the values for m and n come from the data introduced by the user (not therefore hardcoded in the file) in the input tables, and the same happens with the formula after entering it from SAT plugin and convert into the input table format. The custom app defines the mechanism to convert those data in the params for P-Lingua (m, n, nvals, and variable{i}, clause{i}, val{i}, valn{i} for each i from 1 to nvals):
@model<infEnv_symport_antiport>
def main()
{
/* Notice that the sentences let assigning ad-hoc values to n and m are not present yet*/
call module_alphabet(n,m);
call module_init_conf(n,m);
call module_rules(n,m);
call module_input();
}
...
def define_input()
{
@ms(1) += _x{variable{i},clause{i}}*valn{i}, x{variable{i},clause{i}}*val{i} : 1<=i<=nvals;
}
Adapted files¶
- Custom application, defining the needed input and output tables for SAT problem solved with P systems with active membranes.
- Model file, P-Lingua file with the parametrized file specifying the family of P systems for solving the partition problem. The custom interface enable the user to introduce the data corresponding to each different scenario.
- Scenario file, for a specific instance of the problem (that is, a specific P system and SAT formula).
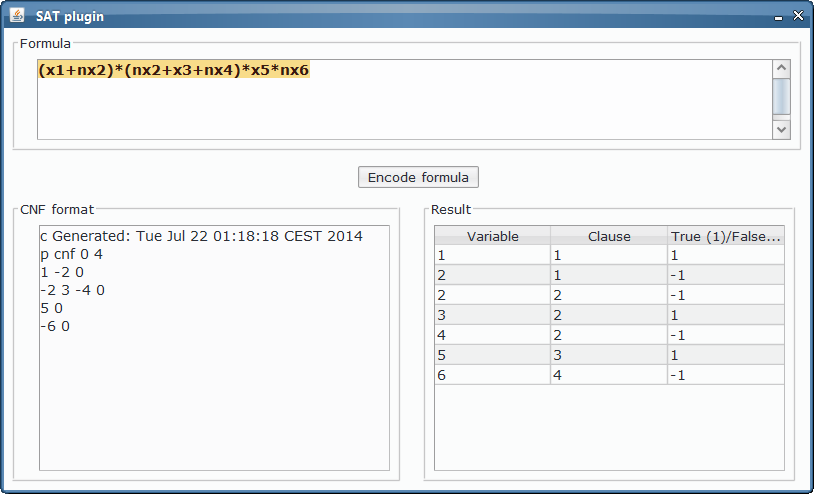
SAT plugin¶
The custom app allows the end user the introduction of the values for n and m to instantiate the P system, along with the formulas by input tables. However, a more natural way of entering the information is provided by SAT plugin: