SAT - P systems with Symport/Antiport Rules and Membrane Division Rules¶
Description¶
Well-known problem SAT, solved with P systems with Symport/Antiport Rules and Membrane Division Rules.
Model in P-Lingua¶
The corresponding P-Lingua file is presented below. This is a parameterized version of the model, to run with the custom app based on MeCoSim, applicable to any input formula given visually, without altering the code:
@model<infEnv_symport_antiport>
def main()
{
call module_init_conf(n,m);
call module_rules(n,m);
call module_input_instance();
}
def module_init_conf(n,m)
{
@mu = [[[]'2 []'3]'1]'environment;
@msInfEnv += S;
@msInfEnv += d{i,j,k},_d{i,j,k} : 1 <= i <= n, 1 <= j <= m, 1 <= k <= n - 1;
@msInfEnv += T{i},F{i} : 1 <= i <= n;
@msInfEnv += f{r} : 1 <= r <= n + 2*m;
@msInfEnv += delta{j,r} : 0 <= j <= m, 1 <= r <= n - 1;
@msInfEnv += E{j} : 0 <= j <= m;
@msInfEnv += e{i,j},_e{i,j} : 1 <= i <= n, 1 <= j <= m;
@ms(1) += f{0},yes;
@ms(1) += fp{r} : 1 <= r <= n + 2*m + 1;
@ms(1) += delta{j,0} : 0 <= j <= m;
@ms(2) += a{i} : 1 <= i <= n;
@ms(2) += b,c;
@ms(3) += fp{0},no;
}
def module_rules(n,m)
{
/* R1 */
d{i,j,1}*2[x{i,j}]'1 --> x{i,j}[d{i,j,1}*2]'1 : 1 <= i <= n, 1 <= j <= m;
_d{i,j,1}*2[_x{i,j}]'1 --> _x{i,j}[_d{i,j,1}*2]'1 : 1 <= i <= n, 1 <= j <= m;
d{i,j,k+1}*2[d{i,j,k}]'1 --> d{i,j,k}[d{i,j,k+1}*2]'1 : 1 <= i <= n, 1 <= j <= m, 1 <= k <= n - 2;
_d{i,j,k+1}*2[_d{i,j,k}]'1 --> _d{i,j,k}[_d{i,j,k+1}*2]'1 : 1 <= i <= n, 1 <= j <= m, 1 <= k <= n - 2;
e{i,j}[d{i,j,n-1}]'1 --> d{i,j,n-1}[e{i,j}]'1 : 1 <= i <= n, 1 <= j <= m;
_e{i,j}[_d{i,j,n-1}]'1 --> _d{i,j,n-1}[_e{i,j}]'1 : 1 <= i <= n, 1 <= j <= m;
[E{0},f{n+2*m},yes]'1 --> E{0},f{n+2*m},yes[]'1;
[f{n+2*m},no]'1 --> f{n+2*m},no[]'1;
delta{j,r+1}*2[delta{j,r}]'1 --> delta{j,r}[delta{j,r+1}*2]'1 : 0 <= r <= n - 2, 0 <= j <= m;
E{j}*2[delta{j,n-1}]'1 --> delta{j,n-1}[E{j}*2]'1 : 0 <= j <= m;
f{i+1}[f{i}]'1 --> f{i}[f{i+1}]'1 : 0 <= i <= n + 2*m - 1;
/* R2 */
[a{i}]'2 --> [T{i}]'2 [F{i}]'2 : 1 <= i <= n;
E{1}[b]'2 --> b[E{1}]'2;
E{0}[c]'2 --> c[E{0}]'2;
e{i,j}[E{j},T{i}]'2 --> E{j},T{i}[e{i,j}]'2 : 1 <= i <= n, 1 <= j <= m;
_e{i,j}[E{j},F{i}]'2 --> E{j},F{i}[_e{i,j}]'2 : 1 <= i <= n, 1 <= j <= m;
E{j+1},T{i}[e{i,j}]'2 --> e{i,j}[E{j+1},T{i}]'2 : 1 <= i <= n, 1 <= j <= m - 1;
E{j+1},F{i}[_e{i,j}]'2 --> _e{i,j}[E{j+1},F{i}]'2 : 1 <= i <= n, 1 <= j <= m - 1;
[e{i,m},E{0}]'2 --> e{i,m},E{0}[]'2 : 1 <= i <= n;
[_e{i,m},E{0}]'2 --> _e{i,m},E{0}[]'2 : 1 <= i <= n;
/* R3 */
fp{r+1}[fp{r}]'3 --> fp{r}[fp{r+1}]'3 : 0 <= r <= n + 2*m;
[fp{n+2*m+1},no]'3 --> fp{n+2*m+1},no[]'3;
}
def module_input_instance()
{
/* We define here the input for the P system */
/* Let suppose m = clause number and n = variable numbers */
@ms(1) += _x{variable{i},clause{i}}*valn{i}, x{variable{i},clause{i}}*val{i} : 1<=i<=nvals;
}
Adapting a problem to MeCoSim philosophy¶
As commented, this model solves our problem, in this case SAT, by means of a family of P systems. With P-Lingua, a general-purpose language, parsers and simulators have been provided.
The given P-Lingua file includes the definition of our P system as provided for the designer, and does not provide specific values for m (clauses) and n (variables) nor a specific input for the system (cod(s)) codifying a formula.
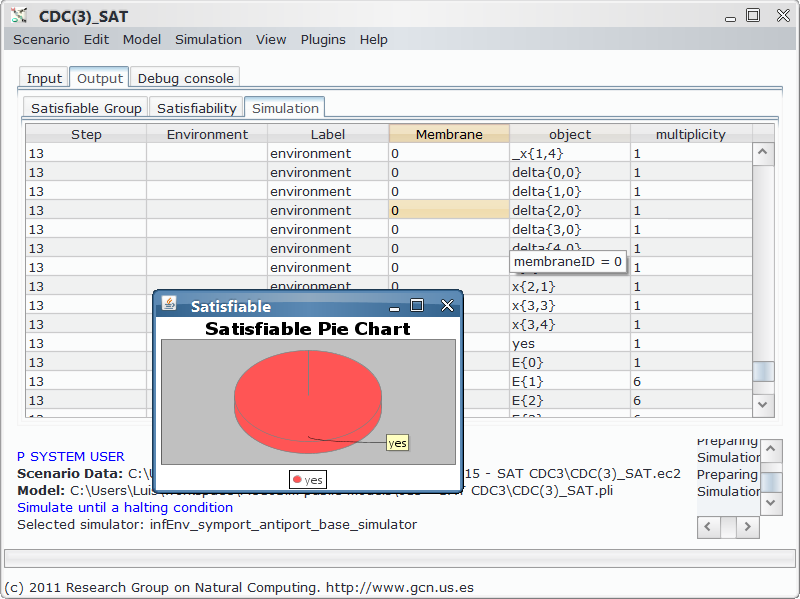
Among the goals of MeCoSim is the clear separation of the roles of end-user and P systems designer, so a custom app is provided defining the inputs for introducing the specific instance of the P system and the given formula, along with the outputs adapted to our problem, thus focusing the attention in solving the problem beyond the meta-analysis of the P system, that is interesting for the designer but probably not for a person trying to know the satisfiability of the P system.
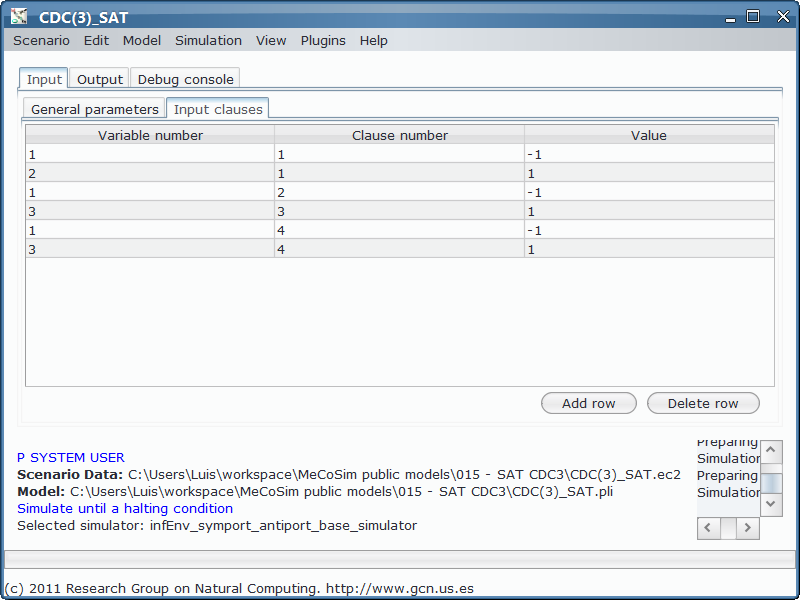
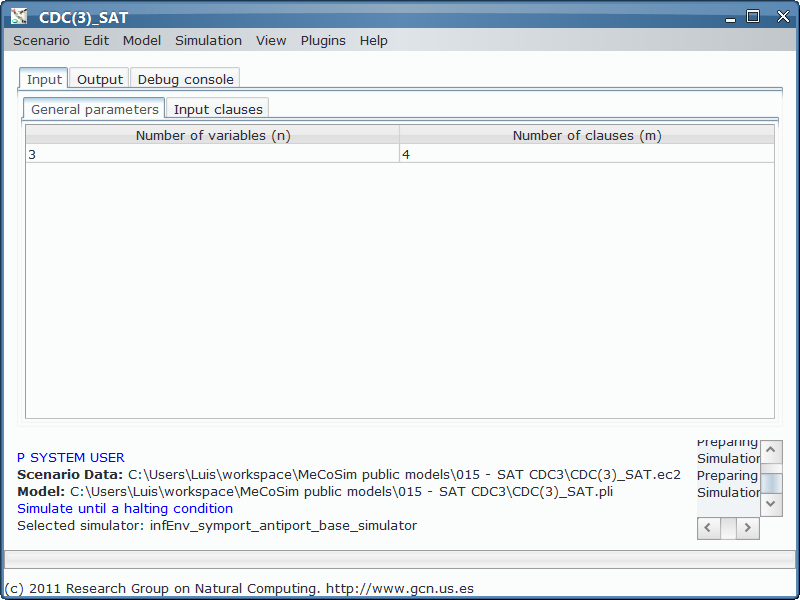
Therefore, the values for m and n come from the data introduced by the user in the input tables (not hardcoded in the file), and the same happens with the formula after entering it from SAT plugin and convert into the input table format. The custom app defines the mechanism to convert those data in the params for P-Lingua (m, n, nvals, and variable{i}, clause{i}, val{i}, valn{i} for each i from 1 to nvals):
@model<infEnv_symport_antiport>
...
def module_input_instance()
{
@ms(1) += _x{variable{i},clause{i}}*valn{i}, x{variable{i},clause{i}}*val{i} : 1<=i<=nvals;
}
Adapted files¶
- Custom application, defining the needed input and output tables for SAT problem solved with P systems with active membranes.
- Model file, P-Lingua file with the parametrized file specifying the family of P systems for solving the partition problem. The custom interface enable the user to introduce the data corresponding to each different scenario.
- Scenario file, for a specific instance of the problem (that is, a specific P system and SAT formula).
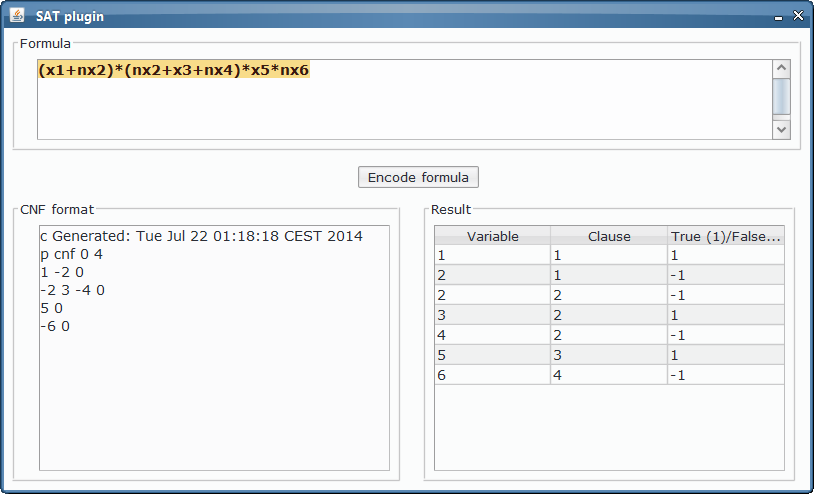
SAT plugin¶
The custom app allows the end user the introduction of the values for n and m to instantiate the P system, along with the formulas by input tables. However, a more natural way of entering the information is provided by SAT plugin: